急遽、カテキョの担当生徒さんが「高校物理の波動が分からない」ということで波動を教えることになった音恩です。
とはいうものの、私が波動の問題を最後に解いたのは2年前…その間、すっかり公式も何もかも忘れてしまいました。そんな私が波動の授業なんかできるのかっ!というわけで、とりあえず予習。
今日も問題。クリックで拡大します。
よく見かける「グラフを読み取る」問題。波動としては定番ですね。
このグラフには2種類あります。どっちも似たような「波」の形をしてるんですけれど、ひとつは「波形」、ひとつは「単振動」のグラフです。
・・・はい、今ちょこっとだけ難しいことを言いました。高校時代、私はどうしてもこの2つのグラフの違いが分からなかったんです。でも今ここでそれを説明してると問題をやる暇がありませんから、とりあえず次にまわすとして…この問題で使用されているのがどっちかという話からはじめます。
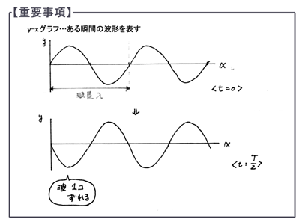
(クリック拡大)
これは私の高校時代のノートの抜粋です。手書きなので図が少々汚いですが、大目に見てくださいませ。
この問題で使われているのは「波形」のグラフです。ナワトビのナワの片方を固定し、もう片方を上下に揺すると波ができますよね。大ナワトビじゃありませんから、回しちゃだめよ。で、ナワを揺すってる調度その瞬間をバチっと写真にとるとどんな風に写るか。そりゃ勿論、ナワはナミナミの形になってると思います。それが、波形なんです。波のカタチ。文字通りですね。
波の要素ってのがいくつかありまして、波形のグラフから読み取れるのは「振幅」と「波長」です。
波長は波の山から山、もしくは谷から谷のキョリということはご存知でしょうか?振幅は、山の高さあるいは谷の深さですね。山と谷の高低差じゃありませんから注意しましょう。
では、問題に移ります。
(1)振幅、波長、周期、速さ
振幅と波長は一瞬で読み取ってください。振幅は2cm、波長は20cmですよ。
次に周期を求めます。これは公式があるので、普通に代入します。
周期と振動数は逆数の関係でしたね。今は、振動数が分かっています。2.5Hzです。
じゃあ周期は
周期=(振動数)-1=1/2.5=0.4s
ですね。
普通のHTMLエディタで分数を書くのはなかなか大変です。指数とかスラッシュとかを駆使して1行に収めてますので、見づらかったらごめんなさい。複雑な式はなるたけきちんとした分数の形で書こうと思いますが、簡単な式までそんなことする時間はないんだ・・・。
今度は速さです。
波の速さの公式はものすご~く重要です。これを覚えていない人は、まず覚えること。簡単だけど、便利な公式です。
v=fλ
見覚えあるでしょう?
この公式に代入するだけでいいんです。fは振動数、λは波長ですからそのまま。
速さ=2.5×20=50cm/s
単位に注意してね。波長が「cm」だから速さも「cm/s」ですが、「m」だったり「nm」だったりしたら速さの単位も変わりますよ。でも振動数は「1秒間」にゆれる数ですから、時間は「s」でいいんですよ。
(2)B点での速度
媒質はそれぞれの点で単振動を行います。
媒質、というのは揺れているモノのことです。水面に石をぶちこんで波ができたのなら、媒質は水。ナワトビのナワを揺すっているのなら、媒質はナワです。
注意したいのは、波は移動していきますが、媒質は移動しないことです。
運動会や何かでウェーブってのを作ったことはありませんか?隣の人が立ち上がったら自分も立ち上がるっていう、アレです。
ウェーブを遠くから見ると波が移っていくように見えますが、実際、ウェーブを作ってる人ってのはその場で立ったり座ったりしてるだけですよね。隣に移動しませんよね。そういうことです。
単振動を思い出してください。
「変位が最大になる点での速さはゼロ」と教わりませんでしたか?
運動の速度の向きが変わる瞬間というのは、速度はゼロになっています。当然です。歩いてきてUターンするとき、一瞬立ち止まりませんか?え、回れ右みたいにくるっと回る?でもくるっと回ってる瞬間ってのは、その場で回ってるかもしれませんが、2次元の運動として見ればその位置から動いてませんよね。速度の向きが変わる瞬間、一度物体はとまってしまう。これは覚えておきましょう。
単振動で、速度の向きが変わるのは変位が最大の点です。変位ってのは、基準の点からどのくらい動いたかです。バネを例にとるなら、みょ〜んと伸びたバネは伸びきったところで一旦止まり、それから逆方向に縮んでいく。伸びきった点で、変位が最大になっている。運動の向きも変わる。そういうことです。
話を波に戻します。波の媒質というのは、その点、つまりA点ならA点で、B点ならB点において単振動を行っています。B点の変位を見てみると、最大になっていることが分かりますね。ということは・・・
今まで長々と語って参りましたが、結局B点での速度はゼロだってことが言いたかったんです。
え、拍子抜けした?
(3)媒質の速度と加速度がyの正の向きに最大の点
これも単振動の基礎知識があれば簡単に解けてしまう問題です。
まず、さっきの説明にもありましたように変位が最大の点の速度はゼロです。じゃあ速度が最大の点ってのはどうなる?
・・・変位が最小です。これは、運動エネルギーと位置エネルギーの兼ね合いの問題です。力学的エネルギー保存の法則ってのを聞いたことがあるでしょう?詳しくは、単振動の解説記事でとりあげるので、とりあえず言葉だけ知っておいてね。
じゃあ媒質の「速さ」が最大の点ってのは、x=0、10、20の点だと分かりますね。だって変位がゼロだもんね。この中で「速度」がプラスの向きに最大の点はどうやって調べようか。
ここで「波のグラフの問題」の解き方のワザを使います。
波をほんのちょこっとだけずらすのです。
 赤い線がずらした後の波です。
赤い線がずらした後の波です。
青い矢印は、x座標において波が正と負のどちらにずれているかを示しています。
例えばx=0では、ずらした後の線は、最初の黒い線の上に来ていますね。ですから、ここの矢印は上向きなのです。逆にx=15では、黒い線の下に赤い線があります。ですから矢印は下向きです。
この矢印は自分で打てるようになりましょう。
速度が「正の向き」ということは、この青い矢印が正の方向に向いていればいいんです。
x=0、10、20の点のうち、矢印が上向きなのは0と20ですから、これが答えになります。
速度が正の向きに最大・・・x=0、20
では加速度が最大の点はどこでしょうか。
自転車をイメージしてください。
走り出すときと、走っている状態を続けるとき、どっちが楽でしょうか?
それは勿論、走り続けるほうが楽ですね。走り出すときには、それなりの「パワー」でペダルを踏まなきゃならない。
ということは、走り出すときのほうが力が必要、ということなんです。
加速度を生み出すのは力です。
つまり、止まっているものを動かすときの方が、動いているものを動かすときより加速度が大きいのです。
勿論、動いているものを止めるときも力は必要ですけどね。
それを踏まえてみてやると、加速度が最大の点というのは、運動していない、つまり変位が最大の点ですね。
x=5、15において、加速度は最大です。x=25でも最大ですが、この問題では「0cmから20cm」と言っているので無視してしまいましょう。
そのうち青い矢印が上を向いているのは・・・x=5ですね。
加速度が正の向きに最大・・・x=5
(4)0.1秒後の波形を書け
「媒質は移動しない」と先ほど言いましたが、波は移動します。
つまり0.1秒経ったときに、この波が右にどのくらい移動しているのかを書けばいいんです。
(1)で波の周期は0.4cmだと出しましたね。周期というのは、波が1波長分進むのに何秒かかるか、です。つまり波は0.4秒で1波長分=20cm進みます。
じゃあ0.1秒だったら・・・?
1/4波長、つまり5cm進みますね。
それを図に描きます。
原点Oのところにあった波の“端っこ”を、x=5cmのところに移動します。
すると0~5cmの間には何もなくなってしまいますから、そこには波の続きを描き加えておきましょう。
答えは
 赤い線のようになります。グレーのグラフは、もともとの波です。
赤い線のようになります。グレーのグラフは、もともとの波です。
(5)t=0としたときの点Aにおける媒質の変位と時刻の関係
要するにA点における単振動のグラフを描け、といっています。
あらら、最初に「単振動のグラフの話は後回しにする」って言いましたが、その話がわからないと解けませんね。
さらっと説明しておきます。
問題に出ているグラフは「波形」です。
波っていうのは常に動いています。動画で見るとすご~くわかりやすいのですが、残念ながら動画は試験問題に印刷できません。
だから、時間か媒質の位置のどちらかの要素を切り捨てて、静止画を作らなきゃなりません。
時間の要素を捨てると、波形のグラフができます。
さっきも言いましたように、波形のグラフは動いている波の写真を撮ったものです。ですから、この波がどのくらいの周期をもっているのかはわかりません。もしかしたらものすごく速いのかもしれないし、ものすごく遅いのかもしれない。(1)で求めた周期は、問題文中に書いてあった「振動数2.5Hz」という数値を使いましたね。わざわざそれを問題文に書いたのは、それを書かなきゃ周期がグラフからは読み取れないからなんです。
では波がどんな速さで動いているのかをグラフにしたい!
速い波ほど山の数が大きくなる、そんなグラフはないものか!
それを表すのが単振動のグラフです。今度は運動している媒質1点に注目します。
言ってみれば、ウェーブを作っている個人に注目しているようなもんです。
このグラフだと波の周期はよく分かります。1波長分進むのに何秒かかるか。その代わり、その波がどんな波長をもっているのかが分かりません。
それぞれの表し方をあわせてみてやると、波の周期も波長も分かるわけですね。
では、いよいよグラフを描いてみましょう。
まず、(4)で0.1秒後の波形を書きました。
今から書こうとしているのはA点に注目したグラフですから、波形のなかでもA点だけ見てくれればよろしい。
A点、つまりx=10の点では変位がマイナスの方向に最大です。振幅は2cmですから、変位は-2cmですね。
では、0.2秒後の波形グラフを、(4)と同じ要領で描いてみましょう。
0.1秒後から、さらに5cm進んだわけですね。
 次は、0.3秒後の波形です。
次は、0.3秒後の波形です。
 このくらいでいいかな。
このくらいでいいかな。
せっかく波形を描きましたが、見るのはx=10のところだけですよ。
t=0.2・・・・・x=10においてy=0
t=0.3・・・・・x=10においてy=+2
t: 0→0.1→0.2→0.3
y: 0→-2→0→+2
縦軸にy、横軸にtをとって、この点をプロットし、なめらかな線でつなぐと
 こんなグラフができました。
こんなグラフができました。
これが、yとtの関係です。
今回は単振動や波のグラフの基礎知識の解説を行わずにいきなり問題演習に入ったので、ちょっと難しかったかもしれません。
富山大の入試問題の類題ですしね。
でも、こういった問題が解けるようになれば、なかなか強みになると思います。
そして思うのですが・・・
復習は大切ですよ!
2年でこの系統の問題の解き方をきれいさっぱり忘れていた自分がいました。
ちなみにこの解説は、高校時代私が使っていた演習ノートに、多少の説明を加えて作成しました。
それから後半の解説で使った、なかなか“滑らかな”グラフですが・・・・
「イラストレーター」というソフトで描きました。慣れないソフトなのでやたらと難しかったですが、これを機にイラレの使い方も覚えていきたいなあ、なんて思っています(^^)
PR
